Problem: Kinematics #4

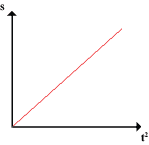
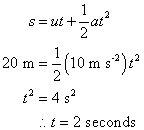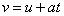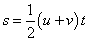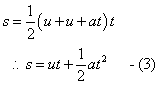A train covers half the distance of its journey with a speed 20 m s^-1 and the other half with a speed of 40 m s^-1. The average speed of the train during the whole journey is
A. 25 m s^-1
B. 27 m s^-1
C. 30 m s^-1
D. 32 m s^-1
E. 35 m s^-1

Solution

Show solution >>

The answer is B.

Let the total distance travelled by the train be d and the time taken for it to complete the first half and second half of the journey be t₁ and t₂ respectively. The distance travelled each half-journey is d/2 and it is the product of their respective travelling velocity and time taken.

For the first half-journey,


For the second half-journey,


Combining the above two equations, we get



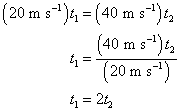
Now we have the relationship between t₁ and t₂, we can eliminate one of them from our calculations. For convenience, let us state the d in terms of t₂ and find the average speed, which is the total distance travelled divided by the total time taken.



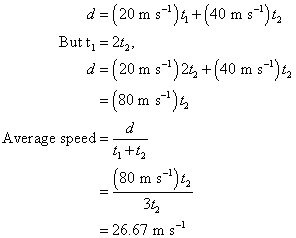
Rounding off to the nearest integer, we have 27 m s^-1.

Hide solution <<

Question source: Malaysia National Physics Competition 2007 (Secondary Level)

Problem: Kinematics #3

The figure above shows a displacement versus time squared (t²) graph for the motion of an object.
Which of the following motion can be represented by this graph?
A. A ball that is travelling at terminal velocity.
B. A ball that is falling freely from a stationary position.
C. A ball that bounces back from the floor.
D. A ball that is travelling on a rough surface.

Solution

Show solution >>

The answer is C.

The graph shows that s is directly proportional to t² or
s ∝ t²
∴ s = kt²

Without modifying the points on the graph, we can manipulate this relationship by dividing both sides by t to become:


But, s/t is the velocity of the object. So,
v = kt

Using the relationship between v and t, a graph can be drawn with similarities with the above graph because the gradient, k remains the same and it too will pass through the origin.

From here, we know that the velocity of the object increases uniformly from zero (acceleration is constant). An object free-falling from a stationary position will experience this kind of motion.

Hide solution <<

Question source: Malaysia National Physics Competition Panel

Problem: Kinematics #2

The figure above shows two objects, P and Q moving with velocities 30 m s^-1 and 20 m s^-1 respectively towards each other on a straight line.
How long, after that instant, will P and Q meet?
A. 100.0 s
B. 83.3 s
C. 20.0 s
D. 13.3 s

Solution

Show solution >>

The answer is C.

Let the distance travelled by P and Q before they meet each other be d₁ and d₂ respectively. Here, we can form an equation:

d1 + d2	= 1000 m
d1	= 1000 m - d2	- (1)

Since we know the speeds of P and Q, their distance travelled is the product of their speed and time taken, t. t is also the time when P and Q meet.

d₁ = (30 m s^-1)t
d₂ = (20 m s^-1)t

Substituting in equation (1),

d1	= 1000 m - d2
(30 m s-1)t 50t m s-1 ∴ t	= 1000 m - (20 m s-1)t = 1000 m = 20 s

Hide solution <<

Question source: Malaysia National Physics Competition Panel

Problem: Kinematics #1

A stone is released from a height of 20 m and allowed to fall in a straight line towards the ground. Ignoring air resistance, calculate
a) the time taken for the stone to reach the ground.
b) the velocity of the stone just before it touches the ground
(Assume that g = 10 m s^-2)

Solution

Show solution >>

The answers for (a) and (b) are 2 seconds and 20 m s^-1 respectively.

This is a problem utilising the equations for uniform acceleration. First, we list out the available information:
u = 0
a = g = 10 m s^-2
s = 20 m

For (a):
We want to find the value of t and we know the values of s, a and u, so we utilise the equation s = ut + ½at²


For (b):
We want to find the value of v and we know the values of s, a and u, so we utilise the equation v² = u² + 2as


Hide solution <<

The Equations for Uniform Acceleration

There are four equations for uniform acceleration (also known as the kinematic equations) which are used to describe the motion of an object:

1.
2.
3.
4.

Where:
u – initial velocity
v – final velocity
a – acceleration
t – time
s – displacement


You may be wondering – why there are four equations instead of one? Notice that each equation has one variable missing. For example, the first equation doesn’t have the variable displacement, s, in it. So, if you were to calculate something that involves displacement, equation 1 is not your choice. Basically, if you know any three of u, v, a, t and s, the others can be found using one or more of the above equations. But take note that you can use these equations only when the acceleration of an object is constant throughout its motion.

It’ll be useful to memorize these formulas if you’re going to solve problems involving motion, but do you know how to derive them? Knowing how to derive these formulas is useful because you will understand how these equations originated and this knowledge acts as a backup in case you forgot any one of them – you just have to derive it and they just appear out of nowhere!


Deriving the Equations

Suppose the velocity of a body increases at a consistent rate from u to v in time t, the body is said to be accelerating uniformly and uniform acceleration a is given by


Since the velocity is increasing steadily, the average velocity is the mean of the initial and final velocities:


If s is the displacement of the body in time t, then the average velocity is equal displacement/time or s/t, so we can say


By substituting equation 1 into equation 2, we have


By rearranging equation 1, we know that t = (v-u)/a. We substitute this value of t into equation 2 and we have


There’re other ways of deriving these equations. Can you find them?


See Also

• Problem: Kinematics #1 - a sample problem that requires the usage of these equations.