Within a certain type of star called a neutron star, the material at the centre has a mass density of 1.0 × 1018 kg m-3. If a small sphere of this material of radius 1.0 × 10-5 m were somehow transported to the surface of the earth, what would be the weight of this sphere? (Assume that g = 10 m s-2)
A. 1000 N
B. 4200 N
C. 4.2 × 104 N
D. 7.0 × 104 N
E. 3.1 × 109 N
Solution
Show solution >>
The answer is C.
From the information given, we need to first find the volume of this sphere, then find its mass and lastly calculate its weight. Therefore, we need the following formulas:

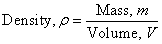
Weight, W = mg
where r is the radius of the sphere.
Step 1- Finding the volume of the sphere:
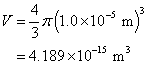
Step 2 - Finding the mass of the sphere:
The second formula can be rearranged to m = Vρ, so
Step 3 - Finding the weight of the sphere:
Rounding off, we have W = 4.2 × 104 N.
Hide solution <<
From the information given, we need to first find the volume of this sphere, then find its mass and lastly calculate its weight. Therefore, we need the following formulas:
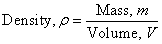
Weight, W = mg
where r is the radius of the sphere.
Step 1- Finding the volume of the sphere:
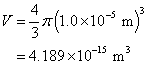
Step 2 - Finding the mass of the sphere:
The second formula can be rearranged to m = Vρ, so
| m | = (4.189 × 10-15 m3)(1.0 × 1018 kg m-3) = 4.189 × 103 kg |
Step 3 - Finding the weight of the sphere:
| W | = (4.189 × 103 kg)(10 m s-2) = 4.189 × 104 kg m s-2 = 4.189 × 104 N |
Rounding off, we have W = 4.2 × 104 N.
Hide solution <<
Question source: Malaysia National Physics Competition 2007 (Secondary Level)

