A stone is released from a height of 20 m and allowed to fall in a straight line towards the ground. Ignoring air resistance, calculate
a) the time taken for the stone to reach the ground.
b) the velocity of the stone just before it touches the ground
(Assume that g = 10 m s-2)
Solution
Show solution >>
The answers for (a) and (b) are 2 seconds and 20 m s-1 respectively.
This is a problem utilising the equations for uniform acceleration. First, we list out the available information:
u = 0
a = g = 10 m s-2
s = 20 m
For (a):
We want to find the value of t and we know the values of s, a and u, so we utilise the equation s = ut + ½at2
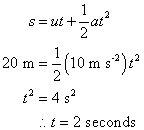
For (b):
We want to find the value of v and we know the values of s, a and u, so we utilise the equation v2 = u2 + 2as

Hide solution <<
This is a problem utilising the equations for uniform acceleration. First, we list out the available information:
u = 0
a = g = 10 m s-2
s = 20 m
For (a):
We want to find the value of t and we know the values of s, a and u, so we utilise the equation s = ut + ½at2
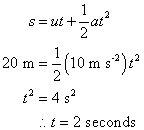
For (b):
We want to find the value of v and we know the values of s, a and u, so we utilise the equation v2 = u2 + 2as

Hide solution <<


1 comment:
Given:
d = 20.0 m
g = 10 m/s^2
vi = 0 m/s
Sol'n:
a.) d = vi*t + (g*t^2)/2
20.0 m= (0)*t + ((10 m/s^2)*t^2)/2
20.o m= (5.0 m/s^2)* t^2
4.0 s^2 = t^2
t = 2 sec
b.) vf = vi + gt
vf = 0 m/s + (10 m/s^2)*(2 s)
vf = 20 m/s
Post a Comment