A cube of ice is floating in a salt solution of density 1.25 times the density of pure water in a beaker. When the ice melts, the level of the solution in the vessel
A. rises
B. falls
C. remains unchanged
D. falls at first and then rises to the same height as before
Solution
Show solution >>
The answer is A.
A non-mathematical explanation would be that since the ice is floating, its mass would be the same as the mass of salt water displaced by it, as per Archimedes’ principle. Now consider the ice melted where the resulting water gradually “fills in” the space in the solution once occupied by the ice. The mass of the resulting water would still be the same as the mass of salt water displaced earlier, but the resulting water will occupy a larger space compared to the salt water displaced, because its density is lower (density is mass per unit volume). Hence the solution level rises.
A mathematical proof is as follows:
Mass of displaced salt solution = Mass of resulting water
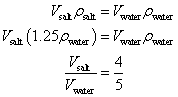
This shows that the resulting water occupies more space compared to the displaced salt water in the ratio 5:4.
Hide solution <<
A non-mathematical explanation would be that since the ice is floating, its mass would be the same as the mass of salt water displaced by it, as per Archimedes’ principle. Now consider the ice melted where the resulting water gradually “fills in” the space in the solution once occupied by the ice. The mass of the resulting water would still be the same as the mass of salt water displaced earlier, but the resulting water will occupy a larger space compared to the salt water displaced, because its density is lower (density is mass per unit volume). Hence the solution level rises.
A mathematical proof is as follows:
Mass of displaced salt solution = Mass of resulting water
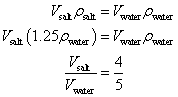
This shows that the resulting water occupies more space compared to the displaced salt water in the ratio 5:4.
Hide solution <<
Question source: Malaysia National Physics Competition 2007 (Secondary Level)

