One of the most important mathematical operations in physics is finding the relationship between variables. Through the study of these relationships, we can know how a change in one variable affects another variable, thus enabling us to make predictions and conclusions easily.
For example, an automobile maker will want to know how the mass of a car affects its acceleration, so that they can design cars with optimum performance.
Direct Proportion
Suppose that in an experiment four sets of readings are obtained for the quantities of x, y, p and q as in the tables below.
x | 1 | 2 | 3 | 4 |
y | 1 | 2 | 3 | 4 |
p | 1 | 2 | 3 | 4 |
q | 3 | 6 | 9 | 12 |
Table 2
In Table 1, we see that when x is doubled, y doubles; when is x trebled, y trebles; when x is halved, y halves and so on.
Similarly in Table 2, when p is doubled, q doubles; when p is trebled, q trebles; when p is halved, q halves and so on.
Now, two graphs are plotted using the values in Table 1 and Table 2, as shown below:
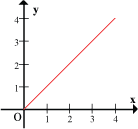 | 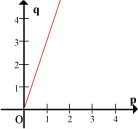 |
Since both graphs are similar in the sense that they are straight line graphs passing through the origin, the relationship of x with y and p with q are somewhat similar. We say that both pairs of variables are directly proportional to each other or varies directly with each other. In symbols,
x ∝ y and p ∝ q
But there is a difference in gradient (slope) between the two graphs, as illustrated above. When we want to define the relationship between the two variables exactly, we have to take into account this difference. Because they are straight line graphs passing through the origin,
where x and y are the x and y values of any point on the graphs.
The constant obtained is called the constant of proportionality or variation and is given a symbol, such as k, so that the relation between y and x can be summed up by the equation

Therefore, we can conclude that the relationship between x and y in Table 1 is
y = x
(k = 1)
The relationship between p and q in Table 2 is
p = 3q
(k = 3)
Notes:
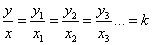
- The constant of proportionality defines how y increases with x. Every increase of 1 unit of x will result in k increase in y.
- In practice, because of inevitable experimental errors, the readings seldom show the relation so clearly as here.
- Assuming that there are points (x1, y1), (x2, y2), (x3, y3), … and x ∝ y, we can say
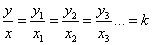
or y1 = kx1, y2 = kx2, y3 = kx3…
Examples of physical quantities that vary directly with each other are:
- Force and mass
- Work done and force
- Speed of wave and its frequency


No comments:
Post a Comment