The Relationship between Variables (Part II)

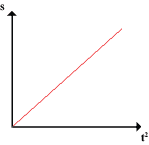
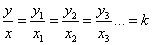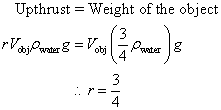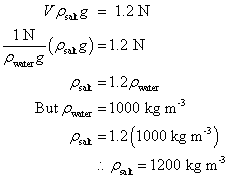This article is a continuation from Part I, which discusses about direct proportion.

Inverse Proportion

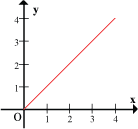
Two sets of readings for the quantities x and y are given in the table below.

x	3	4	6	12
y	4	3	2	1

Here, when x is doubled, y is halved; when x is trebled, y is one-third its previous value and so on.

We say that y is inversely proportional to x, or y varies inversely as x, that is

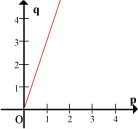
The graph of y versus x is as shown:

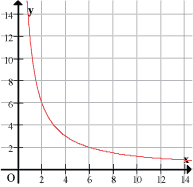
Notice that the product of x and y is the same for every point (12 in this case). Hence this product is known as the constant of proportionality or variation and it is given a symbol such as k. Therefore, we can write the exact relationship between x and y as

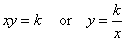
Assuming that there are points (x₁, y₁), (x₂, y₂), (x₃, y₃), …, we can say

xy = x₁y₁ = x₂y₂ = x₃y₃ … = k

Notes:

1. When a variable is proportional to two or more variables, we can represent this relationship as a joint variation. For example,
   When
   y ∝ x and y ∝ z
   therefore
   y ∝ xz or y = kxz
   
   When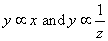
   
   therefore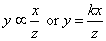
   

2. In every proportional relationship, the converse is also true. For example,

If y ∝ x, then x ∝ y.

Examples of physical quantities that vary inversely with each other are:

• Pressure and volume
• Frequency and periodic time
• Gravitational force and the distance squared

To be continued…

Problem: Kinematics #3

The figure above shows a displacement versus time squared (t²) graph for the motion of an object.
Which of the following motion can be represented by this graph?
A. A ball that is travelling at terminal velocity.
B. A ball that is falling freely from a stationary position.
C. A ball that bounces back from the floor.
D. A ball that is travelling on a rough surface.

Solution

Show solution >>

The answer is C.

The graph shows that s is directly proportional to t² or
s ∝ t²
∴ s = kt²

Without modifying the points on the graph, we can manipulate this relationship by dividing both sides by t to become:


But, s/t is the velocity of the object. So,
v = kt

Using the relationship between v and t, a graph can be drawn with similarities with the above graph because the gradient, k remains the same and it too will pass through the origin.

From here, we know that the velocity of the object increases uniformly from zero (acceleration is constant). An object free-falling from a stationary position will experience this kind of motion.

Hide solution <<

Question source: Malaysia National Physics Competition Panel

The Relationship between Variables (Part I)

One of the most important mathematical operations in physics is finding the relationship between variables. Through the study of these relationships, we can know how a change in one variable affects another variable, thus enabling us to make predictions and conclusions easily.

For example, an automobile maker will want to know how the mass of a car affects its acceleration, so that they can design cars with optimum performance.


Direct Proportion

Suppose that in an experiment four sets of readings are obtained for the quantities of x, y, p and q as in the tables below.

x	1	2	3	4
y	1	2	3	4

Table 1

p	1	2	3	4
q	3	6	9	12

Table 2


In Table 1, we see that when x is doubled, y doubles; when is x trebled, y trebles; when x is halved, y halves and so on.

Similarly in Table 2, when p is doubled, q doubles; when p is trebled, q trebles; when p is halved, q halves and so on.

Now, two graphs are plotted using the values in Table 1 and Table 2, as shown below:

Since both graphs are similar in the sense that they are straight line graphs passing through the origin, the relationship of x with y and p with q are somewhat similar. We say that both pairs of variables are directly proportional to each other or varies directly with each other. In symbols,

x ∝ y and p ∝ q

But there is a difference in gradient (slope) between the two graphs, as illustrated above. When we want to define the relationship between the two variables exactly, we have to take into account this difference. Because they are straight line graphs passing through the origin,

where x and y are the x and y values of any point on the graphs.

The constant obtained is called the constant of proportionality or variation and is given a symbol, such as k, so that the relation between y and x can be summed up by the equation


Therefore, we can conclude that the relationship between x and y in Table 1 is
y = x
(k = 1)

The relationship between p and q in Table 2 is
p = 3q
(k = 3)

Notes:

1. The constant of proportionality defines how y increases with x. Every increase of 1 unit of x will result in k increase in y.
2. In practice, because of inevitable experimental errors, the readings seldom show the relation so clearly as here.
3. Assuming that there are points (x₁, y₁), (x₂, y₂), (x₃, y₃), … and x ∝ y, we can say

or y₁ = kx₁, y₂ = kx₂, y₃ = kx₃…

Examples of physical quantities that vary directly with each other are:

• Force and mass
• Work done and force
• Speed of wave and its frequency

>> Continue to Part II

Problem: Kinematics #2

The figure above shows two objects, P and Q moving with velocities 30 m s^-1 and 20 m s^-1 respectively towards each other on a straight line.
How long, after that instant, will P and Q meet?
A. 100.0 s
B. 83.3 s
C. 20.0 s
D. 13.3 s

Solution

Show solution >>

The answer is C.

Let the distance travelled by P and Q before they meet each other be d₁ and d₂ respectively. Here, we can form an equation:

d1 + d2	= 1000 m
d1	= 1000 m - d2	- (1)

Since we know the speeds of P and Q, their distance travelled is the product of their speed and time taken, t. t is also the time when P and Q meet.

d₁ = (30 m s^-1)t
d₂ = (20 m s^-1)t

Substituting in equation (1),

d1	= 1000 m - d2
(30 m s-1)t 50t m s-1 ∴ t	= 1000 m - (20 m s-1)t = 1000 m = 20 s

Hide solution <<

Question source: Malaysia National Physics Competition Panel

Problem: Materials #2

The density of an object is ¾ of the density of water. If the object is floating on the water surface, then the ratio between the volume of object above the water surface and the volume of object below the water surface is
A. 1:4
B. 1:3
C. 3:4
D. 4:3

Solution

Show solution >>

The answer is B.

This is a problem that requires the application of Archimedes’ principle.

We know that the density of the object is ¾ of the density of water, so the weight of the object, W is given by


Where
V_obj – Volume of the object
ρ_water – Density of water
g – The acceleration due to gravity

Because the object is floating freely,
Upthrust = Weight of the object

But upthrust depends on the volume of object submerged. Let r be the ratio between the volume of object submerged and the total volume of the object, so that rV_obj is the volume of object submerged.




We can conclude that ¼ of the object is above the water surface and ¾ of the object is below the water surface.

Therefore, the ratio between the volume of object above the water surface and the volume of object below the water surface is 1:3.

Hide solution <<

Question source: Malaysia National Physics Competition Panel

Problem: Materials #1

An object has a weight of 4 N in air, 3 N in water and 2.8 N in a salt solution. If the density of water is 1000 kg m^-3, the density of the salt solution is
A. 830 kg m^-3
B. 1070 kg m^-3
C. 1200 kg m^-3
D. 1430 kg m^-3

Solution

Show solution >>

The answer is C.

This is a problem that requires the application of Archimedes’ principle.

The object has a weight of 4 N in air. Because the upthrust on the object when it is in air is negligible, we can say that the weight of the object is 4 N.

When the object is (completely immersed) in water, its weight is 3 N, so it experiences an apparent loss of weight of 1 N due to the upthrust acting on the object.

Upthrust = Apparent loss of weight
and
Upthrust = Vρ_waterg

Where
V – volume of the object
ρ_water – density of water
g – the acceleration due to gravity

Now the object is immersed in a salt solution with density ρ_salt and its weight becomes 2.8 N. It experiences an apparent loss of weight of 1.2 N, therefore
Upthrust = Vρ_saltg = 1.2 N - (2)

Because the volume of object remains the same, we substitute equation 1 into equation 2.

Hide solution <<

Question source: Malaysia National Physics Competition Panel