The density of an object is ¾ of the density of water. If the object is floating on the water surface, then the ratio between the volume of object above the water surface and the volume of object below the water surface is
A. 1:4
B. 1:3
C. 3:4
D. 4:3
Solution
Show solution >>
The answer is B.
This is a problem that requires the application of Archimedes’ principle.
We know that the density of the object is ¾ of the density of water, so the weight of the object, W is given by
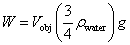
Where
Vobj – Volume of the object
ρwater – Density of water
g – The acceleration due to gravity
Because the object is floating freely,
Upthrust = Weight of the object
But upthrust depends on the volume of object submerged. Let r be the ratio between the volume of object submerged and the total volume of the object, so that rVobj is the volume of object submerged.
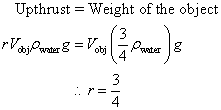
We can conclude that ¼ of the object is above the water surface and ¾ of the object is below the water surface.
Therefore, the ratio between the volume of object above the water surface and the volume of object below the water surface is 1:3.
Hide solution <<
This is a problem that requires the application of Archimedes’ principle.
We know that the density of the object is ¾ of the density of water, so the weight of the object, W is given by
Where
Vobj – Volume of the object
ρwater – Density of water
g – The acceleration due to gravity
Because the object is floating freely,
Upthrust = Weight of the object
But upthrust depends on the volume of object submerged. Let r be the ratio between the volume of object submerged and the total volume of the object, so that rVobj is the volume of object submerged.
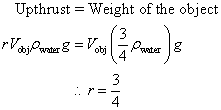
We can conclude that ¼ of the object is above the water surface and ¾ of the object is below the water surface.
Therefore, the ratio between the volume of object above the water surface and the volume of object below the water surface is 1:3.
Hide solution <<
Question source: Malaysia National Physics Competition Panel


No comments:
Post a Comment