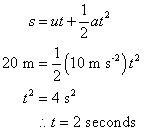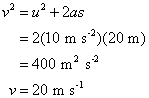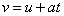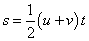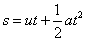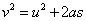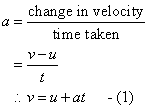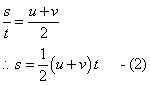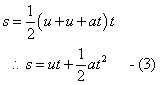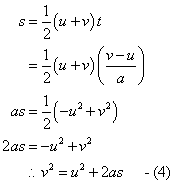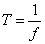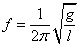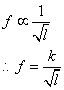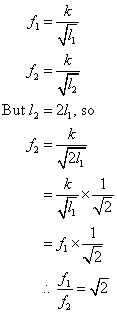Archimedes' Principle Explained

Archimedes' principle is a law that explains buoyancy or upthrust. It states that

When a body is completely or partially immersed in a fluid it experiences an upthrust, or an apparent loss in weight, which is equal to the weight of fluid displaced.

According to a tale, Archimedes discovered this law while taking a bath. After making this discovery, he is said to have leapt out of his bathtub and ran through the streets of Syracuse naked shouting "Eureka!".

An object experiences upthrust due to the fact that the pressure exerted by a fluid on the lower surface of a body being greater than that on the top surface, since pressure increses with depth. Pressure, p is given by p = hρg, where:
h is the height of the fluid column
ρ (rho) is the density of the fluid
g is the acceleration due to gravity


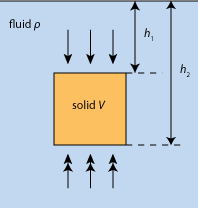Let us confirm this principle theoretically. On the figure on the left, a solid block is immersed completely in a fluid with density ρ. The difference in the force exerted, d on the top and bottom surfaces with area a is due to the difference in pressure, given by

d = h₂aρg – h₁aρg = (h₂ – h₁)aρg

But (h₂– h₁) is the height of the wooden block. So, (h₂ – h₁)a is the volume of the solid block, V.

d = Vρg
∴ Upthrust = Vρg

In any situation, the volume of fluid displaced (or the volume of the object submerged) is considered to calculate upthrust, because (h₂ – h₁) is the height of the solid block only when it is completely immersed. Furthermore, the pressure difference of the fluid acts only on the immersed part of an object.

Now, moving back to Vρg. Since V is the volume of fluid displaced, then the product of V, ρ and g is the weight of the fluid displaced. So, we can say that

Upthrust = Weight of the fluid displaced

Compare this conclusion with the statement above summarising Archimedes' principle. Are they the same? Well, not totally. The “apparent loss in weight” was not mentioned in my explanation.

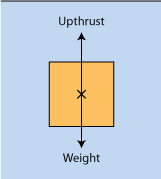In the figure on the left, there are arrows on the top and bottom of the solid block. The downward arrow represent the weight of the block pulling it downwards and the upward arrow represent the upthrust pushing it upwards. If one were to measure the weight of the solid block when it is immersed in the fluid, he will find that the weight of the block is less than that in air. There is a so-called “apparent loss in weight”, because the buoyant force has supported some of the block’s weight.

Weight in air – Upthrust	=	Weight in fluid
Upthrust	=	Weight in air - Weight in fluid

∴ Upthrust = Apparent loss in weight


Objects Floating Freely

When an object is floating freely (i.e. neither sinking nor moving vertically upwards), then the upthrust must be fully supporting the object’s weight. We can say

Upthrust on body = Weight of floating body

By Archimedes’ principle,

Upthrust on body = Weight of fluid displaced

Therefore,

Weight of floating body = Weight of fluid displaced

This result, sometimes called the “principle of floatation”, is a special case of Archimedes’ principle and can be stated:

A floating body displaces its own weight of fluid.

If a body cannot do this, even when completely immersed, it sinks.


See Also

• Problem: Materials #1 - a sample problem involving Archimedes' principle.
• Materials - for related articles and problems.

Problem: Kinematics #1

A stone is released from a height of 20 m and allowed to fall in a straight line towards the ground. Ignoring air resistance, calculate
a) the time taken for the stone to reach the ground.
b) the velocity of the stone just before it touches the ground
(Assume that g = 10 m s^-2)

Solution

Show solution >>

The answers for (a) and (b) are 2 seconds and 20 m s^-1 respectively.

This is a problem utilising the equations for uniform acceleration. First, we list out the available information:
u = 0
a = g = 10 m s^-2
s = 20 m

For (a):
We want to find the value of t and we know the values of s, a and u, so we utilise the equation s = ut + ½at²


For (b):
We want to find the value of v and we know the values of s, a and u, so we utilise the equation v² = u² + 2as


Hide solution <<

The Equations for Uniform Acceleration

There are four equations for uniform acceleration (also known as the kinematic equations) which are used to describe the motion of an object:

1.
2.
3.
4.

Where:
u – initial velocity
v – final velocity
a – acceleration
t – time
s – displacement


You may be wondering – why there are four equations instead of one? Notice that each equation has one variable missing. For example, the first equation doesn’t have the variable displacement, s, in it. So, if you were to calculate something that involves displacement, equation 1 is not your choice. Basically, if you know any three of u, v, a, t and s, the others can be found using one or more of the above equations. But take note that you can use these equations only when the acceleration of an object is constant throughout its motion.

It’ll be useful to memorize these formulas if you’re going to solve problems involving motion, but do you know how to derive them? Knowing how to derive these formulas is useful because you will understand how these equations originated and this knowledge acts as a backup in case you forgot any one of them – you just have to derive it and they just appear out of nowhere!


Deriving the Equations

Suppose the velocity of a body increases at a consistent rate from u to v in time t, the body is said to be accelerating uniformly and uniform acceleration a is given by


Since the velocity is increasing steadily, the average velocity is the mean of the initial and final velocities:


If s is the displacement of the body in time t, then the average velocity is equal displacement/time or s/t, so we can say


By substituting equation 1 into equation 2, we have


By rearranging equation 1, we know that t = (v-u)/a. We substitute this value of t into equation 2 and we have


There’re other ways of deriving these equations. Can you find them?


See Also

• Problem: Kinematics #1 - a sample problem that requires the usage of these equations.

Problem: Waves #1

The frequency of oscillation of a simple pendulum is f₁. When the length of the pendulum l is increased to 2l, the frequency of oscillation of the simple pendulum is f₂. The value of the ratio f₁/f₂ is


Solution

Show solution >>

The answer is D.

The formula for the periodic time, T of a simple pendulum is given by

and we know that


Therefore, the formula for f of a simple pendulum is given by


Now we know that*

[* refer to this article]

Moving on,



Hide solution <<

Question source: Malaysia National Physics Competition Panel

Getting Started

This post is about getting started in physics in general and also benefiting from the future contents of this blog as promised in the Introduction post.

For high school students studying physics at school, you can use your textbook for reference should any need arises.

For those who have none or intend to self-study, the following sites and online resources should provide you with texts on high school-level physics:

• Light and Matter
• Lectures in Physics (Based on Light and Matter)
• The Physics Classroom
• FHSST Physics
• SparkNotes - Physics Study Guides

Anyhow, it is best to have a physics text/reference book with you if you intend to study physics. The following are some books that will help you get started:

Check out the HSPL Store for more Physics books.

Introduction

This is another blog brought to you by InfoFries. This blog aims to help high school physics students cope with their physics lessons, guide them through their examinations and perhaps lead them to success in the field of physics in the future. This shall be done by placing great emphasis on the understanding of basic concepts.

The articles posted here are meant to supplement existing physics curricula and may not appear in particular order. The problems here promote analytical thinking and problem solving skills, and thus are not exam-oriented. Also, this blog will feature problems from physics contests and competitions so that those interested in participating in any of them can test their knowledge.

Finally, this blog also aims to promote physics as an interesting field of study. All content - except announcement posts - will be posted by me under the name W. Jaylee.


See Also

• Getting Started - learn how to get started in physics and make full use of this site.